Information Theory
Module ID
Ε701
Semester
7
Hours/Week - ECTS
4 – 5
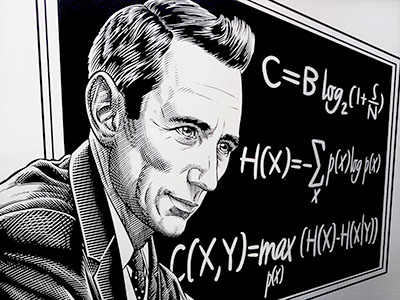
Konstantinos Chaikalis
Associate Professor
Learning Outcomes
This course introduces students to Shannon’s information theory, the mathematical basis of telecommunications.
By the end of the course, students should be able to solve source coding and channel coding problems, illustrate fundamental issues in the field of telecommunications and solve related problems optimization. Typically, students will have acquired the following skills:
- Understanding the nature of entropy and coding principles, as well as channel capacity and rate-alteration theory for discrete and continuous sources.
- Ability to calculate relevant information quantities for selected sources and channels.
- Optimization of multi-source/multi-channel system parameters.
- Presentation and explanation of results in technical terms and in a professional manner.
- The qualifications to continue further in more specialized, closely related subjects.
Indicative Module Content
Topics covered include the source-channel communication model, the axiomatic model for defining uncertainty and entropy, important information quantities such as joint entropy, conditional entropy, relative entropy and mutual information, informational equalities and inequalities, the asymptotic equidistribution principle , entropy rate, entropy of Markov chains, instantaneously decodable and prefix codes, Kraft/McMillan inequalities, Shannon’s source coding theorems, Huffman entropy coding, Shannon, Shannon-Fano, Shannon-Fano-Elias and numerical coding, the mathematical definition of a channel communication, mutual information and its importance in communications, channel capacity, channel coding, Shannon’s channel coding theorems, symmetric channel capacity, channels with feedback, continuous sources and differential entropy, Gaussian channel, continuous channel capacity, water filling principle, theory rate-of-change, its rate-of-change theorems
Shannon, rate-change curves for a Gaussian source with square-error distance metric and a Bernoulli source with Hamming distance, multiple source quantization, reverse water filling principle, Arimoto-Blahut algorithms for calculating channel capacity and rate-change function, network coding.

